Mechanics for the Practitioner and the Thrower

Discus Throw Essentials
Mechanics for the Practitioner and the Thrower

By: Dr. Andreas Maheras

Originally Published in Techniques Magazine - Provided by: USTFCCCA

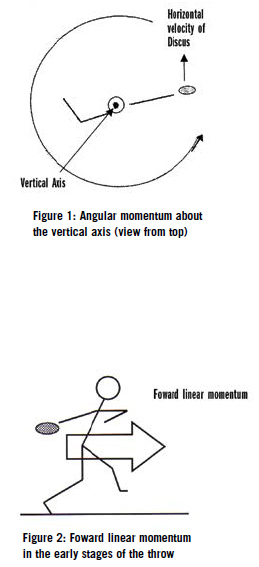
The mechanics of discus throwing is not yet fully understood. Based on the information available to date however, some mechanical elements present the most salient technical points in the course of a discus throw. The points presented here do not represent all technical issues encountered in discus throwing but they do constitute the frame upon which a sound technical pattern should be developed and they do make up the essential elements that a practitioner should have in mind and upon which the throwing execution should be judged as effective and efficient or not. In this direction, it is important not to lose sight of what really matters in discus throwing, at least from a mechanical point of view, and what the practitioner and the thrower are really after during a proper execution of the throw.

BRIEF OVERVIEW OF SPEED GENERATION IN DISCUS THROWING
During the throw the feet exert forces on the ground and the ground react equally and opposite on the feet. Those forces generate linear momentum in the early stages of the throw as the system translates hori-zontally across the circle (see figure 1). During the delivery, the thrower loses some of that momentum and obtains vertical linear momen- tum. The result of the forward and upward linear momentum is a con-tribution to the speed of the discus at release. However, most of the discus speed is due to momentum contributions relative to the center of mass the thrower + discus system. This is where the angular momentum of the thrower, the discus and the combined, thrower+discus, angular momentum come into play. There is angular momentum in two different directions. First, around the vertical axis, which is responsible for imparting horizontal velocity to the discus (see figure 2) and, second around the horizontal axis, which is responsible for imparting vertical velocity to the discus.

On average, the forward linear momentum of the system accounts for approximately 6 percent of the horizontal speed of the discus at release with the remaining 94 percent contributed by the angular momentum around the vertical axis. Similarly, the upward linear momentum accounts for approximately 10 percent of the vertical speed of the discus at release, with the remaining 90 percent contributed by the angular momentum around the horizontal axis. Therefore, most of the speed of the discus is due to angular momentum not linear momentum. Rotary momentum around the vertical axis generates horizontal speed which is transmitted to the discus at release. Angular momentum around the horizontal axis generates vertical speed which is transmitted to the discus during the second half of the delivery phase. Very little of either of those two momentums is obtained from the ground during the time of release. For the most part, they are obtained from the ground during the earlier phases of the throw. That is, the momentum around the vertical axis is generated during the first double support and single support phases and, the momentum around the horizontal axis is generated during the second half of the single support phase on the right foot and the first half of the delivery phase. The angular momentum is stored in the body of the thrower where it expresses itself as a rotation of the body, before being imparted to the discus during the end of the throw. For that reason, the major emphasis should always been given to the rotary aspects of the throw, but without ignoring the linear aspects of it (for more details regarding momentum generation in discus throwing, see Maheras 2008).

BACK OF THE CIRCLE
1. The Shifting of the System's Center of Mass Toward the Left Foot. Theoretically, the thrower should shift the center of mass to a position that is almost directly over the left foot and then push directly backwards on the ground to obtain a good drive directly forward across the circle which means that the system should have a good amount of horizontal speed at the time the left foot loses contact with the ground. This is essential because this linear horizontal speed will be partially converted to vertical during the delivery phase which will then contribute to the final speed of the discus. If the thrower fails to bring the center of mass close enough to the vertical of the left foot, the thrower should make a strong horizontal drive across the circle in an oblique direction and not directly backwards. This will maintain a good amount of linear horizontal velocity for the system. In this case, pushing directly backwards, will reduce the amount of force the left foot can exert on the ground and consequently it will reduce the horizontal velocity (also see Maheras 2012, for a detailed explanation).

2. The Swinging Action of the Right Leg. After the right foot takes off from the ground in the back of the circle, the right leg should make a wide counter-clockwise rotation around the body and then it should be thrust aggres-sively toward the middle of the circle. This action facilitates the generation of angular momentum around the vertical axis exactly because it aids the left foot to exert forces on the ground which are necessary for the generation of that momentum. The three criteria for the action of the right leg are that it should be thrust under control but a) fast, b) far from the middle of the body and, c) over the longest range possible (see Maheras 2011, for further details).

3. The Swinging Action of the Left Arm. Theoretically and ideally, the action of the left arm in the back of the circle is similar to the function of the right leg. Starting with the moment the discus is at its furthermost point at the end of the winds and until the take off of the left foot, the left arm should make a wide counterclockwise rotation around the body. The left arm should be "thrown" in a controlled manner at high speed, away from the middle of the body and over the longest range possible. The aim again is to facilitate the generation of rotary momentum around the vertical axis. If thrusting the left arm aggressively in the back of the circle causes problems in the course of the throw, then its action may have to be curtailed. However, it should be noted that the left arm contributes approximately one third more than the action of the right leg to the rotation of the system. Therefore, the wise practitioner and athlete should make every effort to take advantage of what the left arm has to offer. It is the combined action of the right leg and the left arm that will determine the total amount of rotary momentum of the system (see Maheras 2011, for more).

MIDDLE OF THE CIRCLE
1. Recovery of the Legs. After the left foot loses contact with the ground, the legs can no longer participate in the genera-tion of rotary momentum. Their task at this point is to increase their own speeds of rotation relative to the rest of the body. This will allow for an earlier planting of the left foot and it will also allow the thrower to arrive at a "wound up" position where the lower parts are rotated significantly ahead of the upper parts and the discus itself. During this airborne phase the thrower should decrease the distance between the center of mass of each leg and the longitudinal axis of the system. This axis passes through the system center of mass and points from the lower part to the upper part of the system. If the system tilts, this axis tilts also. One way to achieve a faster rotation of the legs while airborne is to bring them closer to the axis of rotation (see Maheras 2011, for more).

2. Recovery of the Left Arm. After the left foot take off in the back of the circle, the left arm also becomes unable to contribute to the creation of any angular momentum for the system because there is no contact with the ground. The left arm in this instance should reduce its rate of rotation and decrease its radius of motion. This action of the left arm allows it to transfer part of its own momentum to the rest of the system (legs) where it is needed most (see Maheras 2011, for more).

3. Torsion Angles. The achievement of certain torsion angles, just before the final pulling effort, is of paramount importance in the course of discus throwing. There are six different angles that are formed during the second double support (see Maheras 2014, for more). The angle between the right arm and the right foot at the moment of the single support over the latter is the largest of all and it express-es a well wound up position, which is good, since the ensuing unwinding will help the thrower to transfer angular momentum from the body to the discus. The torsion of the shoulders relative to the hips is also a criterion for an adequate wound up position. Depending on anatomical and also mid section and right arm flexibility factors, a thrower can exhibit less than optimum values in a particular torsion angle but compensate with optimum values in another, thus maintaining a satisfactory overall wound up position.

DELIVERY 1. Second Swinging Action of the Left Arm. After the right foot lands in the middle of the circle, the thrower swings the left arm very dynamically counterclockwise and away from the middle of the body which during the second double support (delivery) has a backward tilt. This action facilitates the generation of angular momentum for the system because it helps the right foot to apply forces on the ground necessary for generating the rotary momentum. During the delivery double support it helps both feet to do the same. Because of the backward tilt, the swinging action of the left arm helps generate a combination of angular momentum about both the vertical and the horizontal axis which is what the thrower is after at this particular point (see Maheras 2011, for more).

2. Second Recovery of the Left Arm. The swinging action of the left arm described above helps the system generate additional momentum which is beneficial. Much of this momentum, however, is initially stored in the left arm itself and unless it is transferred to the discus it will not do the thrower any good. To successfully transfer the momentum from the left arm to the discus, the thrower needs to reduce the angular momentum of the left arm during the delivery. This can be achieved by slowing down the arm's motion or reducing the radius of its motion or both (see Maheras 2011, for more).

3. Downward Forces Against the Ground. There is a relationship between the loss of horizontal speed and the gain of vertical speed of the system's center of mass during the delivery phase. What is observed is a loss of horizontal speed and a gain in vertical speed. The larger the loss of horizontal speed during the delivery, the larger the vertical speed of the system at release. Ideally the system should have a large amount of horizontal velocity at the moment of the left foot contact, which itself is planted aggressively on the ground. If those two conditions exist, then the system will lose some of its horizontal velocity but it will still have enough to contribute to the horizontal velocity of the discus, while at the same time there will be a gain in vertical velocity. This way the left foot is the catalyst for the optimum conversion of horizontal velocity to vertical velocity (see Maheras 2009, for more).

4. Divergence Angle. The divergence angle expresses the difference between the horizontal direction of motion of the center of mass and the horizontal direction of motion of the discus at release. Generally, the motion of the center of mass during the last quarter turn is in a diagonal direction forward and toward the left. The horizontal direction of motion of the discus after release points forward and slightly to the right. The size of the divergence angle determines how much of the horizontal speed of the system during the last quarter turn effectively contributes to the horizontal speed of the discus. The larger the divergence angle the greater the loss in the contribution of the horizontal speed of the system to the horizontal speed of the discus and the distance thrown. Values of over 20 degrees result in considerable loses in distance thrown with a 50 degree angle resulting in a 1.4 to 2.1 meters loss. On the other hand a 10 degree value will result in a loss of only 0.1 meter. In practice, the correct drive of the center of mass across the circle and the correct placement of the left foot in the front of the circle will affect the magnitude of that angle (also see Maheras, 2012).

TECHNICAL POINTS AND SUGGESTIONS
Shift the system center of mass towards the left foot to a point almost directly over it and push directly backwards to obtain a good amount of linear horizontal speed to contribute to the horizontal speed of the discus at release. If shifting directly over the left is not feasible, then push diagonally, not directly backwards, to ensure horizontal velocity generation. Ensure that during the landing on the right of the foot in the middle of the circle there is no significant deceleration and that a good amount of horizontal speed remains in the system during the left foot landing in the front of the circle. Pushing directly backwards which implies a straight forward direction of the center of mass, will also help the thrower keep the divergence angle at a minimum and the contribution of the horizontal velocity to the maximum.

Develop a large amount of rotary momentum around the vertical axis in the back of the circle, after adequately rotating the shoulders clockwise, by swinging both the right leg and the left arm in a dynamic, rotational fashion and, under control. This is the only significant chance the thrower has to generate momentum around the vertical axis. Close to 90 percent of the eventual total momentum is developed in the back of the circle during the first double and single supports. Weak swinging actions of the limbs in the back of the circle will result in inadequate rotary momentum generation. Keep the left arm at shoulder level and allow it to participate in the generation of that momentum. Although a thrower can partially make up for lost momentum during the delivery phase, one cannot fully compensate for lost ground in the back of the circle.

Allow both the right and left leg and left arm to recover and "wrap" close to the axis of rotation during the turn in the middle of the circle. This will enable the system to efficiently store the previously acquired momentum, for later use.

Achieve a well would-up position during the single support over the right foot. This will subsequently allow the thrower to transfer the angular momentum from the body to the discus.

Exert a large downward force against the ground during the double support delivery phase to ensure a vertical reaction and the subsequent acquisition of a good amount of vertical speed to contribute to the vertical speed of the discus.

Ensure a good swinging and a good recovery (block) of the left arm during the delivery of the discus.

A FUNDAMENTAL TECHNICAL EVALUATION OF A THROW
The example that follows shows how an evaluation of a discus throwing technique may read. It assumes that individual analysis data for the athlete are available, and it shows what the main technical issues under examination may be.

• The horizontal translation of the system center of mass was (directly for-ward, or oblique). The contribution of the horizontal speed of the system to the horizontal speed of the discus was (average, or larger or smaller than average).
• The contribution of the vertical speed of the system to the vertical speed of the discus was (large, average, etc.).
• The combined swinging actions of the right leg and left arm in the back of the circle were (good, average etc.).
• The amount of angular momentum around the vertical axis generated in the back of the circle was (small, large, etc.). This was followed by a (large, small! increase, decrease) of that momentum in the front of the circle.
• The thrower kept the legs (tight, far apart) while airborne after the take off in the back of the circle.
• The thrower gave a (large, small, average) amount of horizontal speed to the discus.
• The recovery action of the left arm was (good, average, very good).
• The second swing of the left arm was (good, average, etc), and it did (or did not) slow down enough before release.
• During the single support on the right foot and the double support delivery the thrower acquired a (good, moderate, etc.) amount of angular momentum around the horizontal axis.
• The thrower was (or was not) able to transfer it to the discus which made the vertical speed of the discus (large, small, etc.).
• The thrower was (or was not) able to transfer rotary momentum, around the vertical axis, to the discus.
• The thrower achieved a (good, moderate etc.) wound-up position in the single support on the right foot, while (large, small etc.) angles were observed in the (specific torsion angles).
• The ensuing unwinding (did or did not) help the thrower transfer the angular momentum, around the vertical axis, to the discus.
• The divergence angle between the direc-tions of motion of the system and of the discus was (or was not) large. Therefore the contribution of the horizontal speed of the system to the horizontal speed of the discus was (good, average, etc.).

The technical items mentioned here, as a whole, will dramatically influence the amount of speed that can be imparted to the discus at release. The practitioner and the athlete should be aware of them and make them the framework of the throwing action according to the guidelines given above.

AUTHOR'S NOTE
Decrease of the Radius of the Discus. This is a technical/mechanical element that was proposed by Dapena & Anderst (1997) based on analysis observations of an elite thrower. It could theoretically be introduced to those throwers who can implement it successfully at release. For a given amount of rotary momentum of the discus around the vertical axis, the shorter the distance between the system center of mass and the extension of the line of travel of the discus, the higher the horizontal speed of the discus. By tilting the body toward the left near the instant of release the thrower can shorten the distance between the center of mass and the discus and this way increase the horizontal speed of the discus. It is understood that throwers are usually advised to maintain the longest radius for the entire throw and, rightly so for many of them. For skillful throwers, this advice may need to be modified, so that the radius of the discus is maintained as large as possible during the majority of the duration of the throw with a brief shortening of it, immediately before the discus release, simply because this action will increase the speed of the discus. The important technical point here is to shorten the radius close to the release moment only and not sooner. An experienced practitioner should judge the skill level of the thrower and implement this technique point accordingly but not go out of her way to instruct the thrower to do such a thing.

REFERENCES
Dapena, J., & Anderst, W. (1997). Discus Throw (Men). Scientific Services Project, U.S.A Track & Field. Biomechanics Laboratory, Dept. of Kinesiology, Indiana University.

Maheras, A. (2014). Torsion Angles in Discus Throwing. Techniques for Track and Field & Cross Country, 8 (2), 39-42.

Maheras, A. (2012). The Horizontal Translation in Discus Throwing. Techniques for Track and Field & Cross Country, 5 (4), 33-36.

Maheras, A. (2011). The Function of the Extremities in Discus Throwing. Techniques for Track and Field & Cross Country, 4 (4), 8-16.

Maheras, A. (2008). Momentum Development in Discus Throwing. NTCA Throwers Handbook, J.A. Peterson & Lasorsa R. editors, p.p. 132-136.

BIO: Dr. Andreas Maheras is the throws coach at Fort Hays State University in Kansas and is a frequent contributor to techniques.