Hammer Throwing – Dynamic Aspects of the Lower Extremities

By: Andreas V. Maheras, Ph.D

Originally Published in: Techniques Magazine

Provided by: USTFCCCA

During the course of a hammer throw, the thrower will turn with the hammer three or four times alternating between double and single support. In this fashion, the left foot is always in contact with the ground. The right foot spends a good part of the total turn time off the ground, the actual time depending primarily on the skill of the thrower and also the order of a particular turn. The forces exerted by the feet on the ground will allow the thrower to, in turn, successfully impart the optimum amount of force on the hammer itself. An observation of the action of the right foot in hammer throwers will show that some prefer to execute a "stomping" action, as that foot comes in contact with the ground to complete a turn, while others choose to bring it in contact with the ground in a "softer" or neutral fashion during that phase. the action of the feet, and particularly the right foot, from a dynamic point of view, will be discussed below.

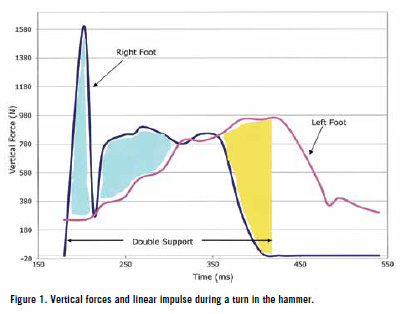
VERTICAL FORCES AND LINEAR IMPULSE

Given that the forces exerted during the turns are mostly on the vertical (Murofushi et. al, 2007), a rudimental examination of those forces follows. Figure 1 shows the vertical force exerted on the right and left feet during a turn. The force exerted on the right foot shows a big spike just after landing, but it is generally so brief, approximately 30 msec., that it will only have a small effect on the generation of angular momentum. What matters more in this figure is the (non-shared) total are under the curve which is shown in blue color for the right foot and gold color for the left foot. This is the linear impulse. In the course of the entire double-support (i.e., the period when the vertical force on the right foot is not zero), the area under the curve is similar for the right foot and the left foot. Initially, the vertical force exerted on the right foot gets a big value (the spike mentioned before). This force then drops almost immediately, and more of less reaches the same value as the vertical force exerted on the left foot. But then it increases again and becomes again clearly larger than the vertical force exerted on the left foot. This continues until roughly half-way into double-support phase. Then the two forces stay about even for a little bit. Finally, the vertical force received by the right foot drops off a lot, as this foot begins to unload (begins to gradually lose contact with the ground), and thus in the final 20-30% of the double-support phase the vertical force received by the left foot becomes much larger than the vertical force received by the right foot.

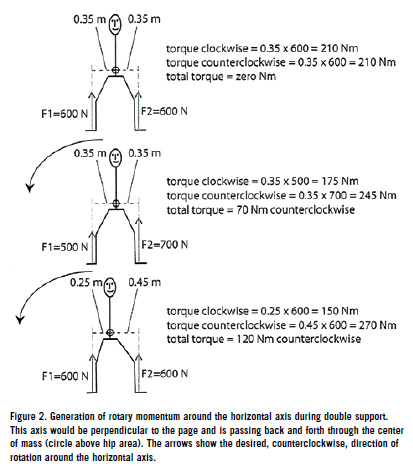
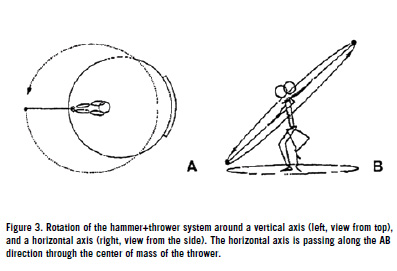
In the early part of the double-support phase the area under the curve is larger for the right foot than for the left foot (blue-shaded area in figure 1), while in the late part of the double-support the area under the curve is larger for the left foot than for the right foot (gold-shaded area in figure 1). Overall, the blue area compensates for the gold area, which means that both feet receive about the same total amount of linear impulse from the ground during the double-support phase. So the average force received by both legs is about the same. So what is happening during the double-support phase according to this graph, is either like what is shown in the top one in figure 2, (which would imply no gain of vertical angular momentum), or it could be like what is shown in the bottom of the same figure (which would imply a gain of vertical angular momentum by having the c.m. closer to the vertical of the right foot than to the vertical of the left foot). In both cases the assumed vertical force is the same for both feet, i.e., 600 N, but it is impossible to know which of the two (top or bottom image in figure 2) is the case in reality, because we don't know where the center of mass was. In all this discussion, the important element is that
the eventual total torque should generate a counterclockwise rotation about the horizontal axis as discussed below.

AXES OF ROTATION AND MECHANISMS OF FORCE GENERATION

During the execution of the turns, the thrower rotates around both a vertical axis (horizontal rotary momentum) and a horizontal axis (vertical rotary momentum), see figure 3, with the majority of the momentum being developed around the horizontal axis (Dapena, 1989, 1984). The right foot's action will primarily generate the rotation about both of those axes, that is, throwers should keep separate in their minds as to what the right foot provokes through its vertical action and what it provokes through its horizontal action. Ideally, a thrower would want as much rotation as possible both about the vertical axis and about the horizontal axis. Hammer throwers therefore, make backward horizontal forces against the ground with their right foot during the turns. Those horizontal forces can be compared to the horizontal forces the rider of a scooter would make to roll forward although the resulting movement in this case is linear as opposed to rotational. We know that horizontal forces do exist because the angular momentum about the vertical axis does increase somewhat during the turns (Dapena, 1989). Doing the "scooter technique" with the right foot is good for achieving hammer speed, but as it happens in the discus throw, it's harder and harder to achieve as the speed of rotation increases in the course of the turns (Rohas-Ruiz, & Gutierrez-Davilla, 2009).

Similarly and more importantly, hammer throwers also make vertical forces around the horizontal axis. What needs to be emphasized and reiterated here is that the majority of the forces exerted on the thrower during the turns are on the vertical or around the horizontal axis. One should also be aware of the mechanism as to how the hammer thrower manages to actively accelerate the hammer to the left
during the turns. The two mechanisms are as follows:

First, the thrower presses harder on the ground with the left foot than with the right foot and/or second, the thrower generates vertical forces on the ground with both feet, but keeps the center of mass of the thrower-hammer system closer to the right foot than to the left foot, instead of half-way between them (figure 2; also for a more detailed explanation see Maheras, 2010). According to those two mechanisms, the net effect, the difference between the two directions,
is necessarily a total torque pointing clockwise, from the thrower's point of view, counterclockwise from the viewer's point of view, which effectively tends to cause the thrower to rotate around the horizontal axis in that direction, which
is towards her own right. From this position, if the thrower accidentally let go of the hammer, she would fall towards her right side. However, the thrower does not let go of the hammer and by pulling on the cable, she will give the hammer an upward acceleration. The eventual practical benefit of the cooperation between the forces exerted by the feet is to create
a counterclockwise torque which will enable the thrower to pull harder upward on the hammer during the upward part of the hammer trajectory resulting in an even greater upward acceleration due to that pulling (Maheras, 2010, 2018).

RIGHT FOOT ACTION

Going back to the action of the right foot which in some throwers can be termed as "stomping" of that foot, it follows that such an action may increasingly, or exclusively, cause the thrower to generate a clockwise torque which will be detrimental to the amount of torque generated counterclockwise. In such a case the "stomping" of the right foot will not be about gaining angular momentum around the horizontal axis, instead "stomping" will make the thrower lose angular momentum about the horizontal axis aligned with the direction of the throw. Ultimately, this is bad for the generation of hammer speed. If the athlete "stomps" the right foot (i.e., if she makes a big downward vertical force on the ground with the right foot), the ground responds by making a big upward vertical force on the right foot. This reaction force, since
it is exerted on the athlete is the one that counts for estimating in which direction the athlete is going to be made to rotate. If the athlete-plus-hammer is already rotating counterclockwise, a "stomping" action will subtract counterclockwise angular momentum from the athlete-plus-hammer system (Dapena, 2018).

Except for the double support, of course, vertical angular momentum is generated during single-support, because the support foot (the left foot) gets a counterclockwise torque from the ground, and the right foot gets nothing, because it's in the air (for more see Maheras, 2010).

The question then arises as to why would anyone stomp hard at all with the right foot as many throwers of various abilities do? It could be that some throwers feel that they need to do this in order to stop their body's fall after the rather small amount of vertical support
that they got from the left foot during the single-support phase. Notice in figure 1 how small the vertical force received by the left foot is during the single-support phase, particularly near the end. Just like the brevity of the right foot spike implied that the stomp probably did not have a big negative effect on the generation of vertical angular momentum, it probably also will not have a big positive effect on stopping the downward translation of the body c.m. But something is better than nothing, so some throwers will do it. In addition,
it is also possible that the throwers may "stomp" the right foot as a result of their intention to plant that foot quickly on the ground as they attempt to accelerate the turning motion.

CONCLUSIONS

From a purely dynamic point of view a hard vertical stomp of the right foot would not have a positive effect on the generation of vertical angular momentum around a horizontal axis. If anything, it should have a negative effect on the generation of that angular momentum. On the other hand, the negative effect would probably not be very big because the stomping produces that very sharp but also very brief initial spike in the vertical force, which due to its brevity does not have a big effect. All in all, stomping or not stomping with the right foot probably does not make a lot of difference for the result of the throw.

Given the above, theoretically, the best way to develop as large rotary momentum as possible about both a vertical and a horizontal axis, would be to plant the right foot quite lightly on the ground, not making a very big vertical force with the right foot (i.e., not stomping), but pulling backward horizontally very hard with the
right foot (i.e., doing the "scooter" action mentioned above).

In case the thrower is able to both "stomp" and, as she does that, also manages to direct that "stomp" backwards to horizontally pull with the right foot, instead
of vertically, that would be desirable as it will enhance the rotation about the vertical axis. However, the thrower will still need to make a reasonable amount of downward force on the ground, pressing down on the ground with a reasonable amount of force, or else she could lose her balance.

REFERENCES

Dapena, J. (1984). The pattern of hammer speed during a hammer throw and influence of gravity on its fluctuations. Journal of Biomechanics, 17 (8), 553-559.

Dapena, J. (1989). Some biomechanical aspects of hammer throwing. Athletics Coach, 23 (3), 12-19.

Dapena, J. (2018). Personal Communication.

Maheras, A. (2010). Reassessing Velocity Generation in Hammer Throwing. I.A.A.F., New Studies in Athletics, 24:4, 71-80.

Maheras, A (2018). Biomechanical Observations in Hammer Throwing.

Techniques for Track and Field & Cross Country, 11 (3), 19-30.

Murofushi, K, Sakurai, S., Umegaki, K, & Takamatsu, J (2007). Hammer acceleration due to the thrower and hammer movement patterns. Sports Biomechanics, 6 (3), 301-314.

Rohas-Ruiz, F.J, & Gutierrez-Davilla,
M (2009). The relation Between Angular

Displacement of the Hammer in the Double Support Phase and its Velocity in the Hammer Throw. Journal of Human Sport & Exercise. 4 (3), 254-261.

Dr. Andreas Maheras is the throws coach at Fort Hays State University in Kansas and is a frequent contributor to techniques.