|
By: Dr. Andreas Maheras Originally Published in: Techniques Magazine Provided by: USTFCCCA
TWO MECHANICAL CONCEPTS Linear momentum is a term that refers to the mechanics of translation of a system. It is directly proportional to the speed of translation of the center of mass (CM) of the system, and it has the same direction as the speed of translation of the CM of the system. Angular momentum (also called "rotary momentum") is a mechanical term that refers to the mechanics of rotation of a system. It is related to how fast a system is rotating (speed of rotation) and how "spread-out" the system is with respect to the axis of rotation. The faster the system is rotating and the more spread-out the system is with respect to the axis of rotation, the larger the angular momentum of the system. To change the angular momentum of a system, it is necessary to exert on that system forces that point off-center to its CM. This is only possible when the system is in direct physical contact with other systems, such as the ground. When a system is not in contact with other systems, no off-center forces are exerted on it, and therefore its angular momentum remains constant; for example, when a discus thrower is in the airborne position just before landing in the middle of the circle. It is possible to transfer angular momentum from one part of a system to another. An example: shortly before release, a discus thrower can transfer counterclockwise angular momentum from the left arm to other parts of the body and eventually to the discus. This will materialize as a slowing down of the counterclockwise speed of rotation of the left arm (and/or a shortening of the radius of the left arm with respect to the middle of the body: less "spread-out"), and a speeding up of the rotations of other body parts (or of the discus). For any given amount of angular momentum that a part of a system has, the closer this part of the system is kept to an axis of rotation, the faster it will tend to rotate around that axis. That happens, for example, after the left foot takes off from the ground following the end of the first single support, when a discus thrower quickly brings both legs near the middle of the body, and the legs tend to rotate faster around the vertical axis. This speeding up of the rotation of the legs will help them to get ahead, from a rotational point of view, of the upper body and of the discus. LINEAR MOMENTUM During a discus throw, the feet make forces on the ground. By reaction, the ground makes equal and opposite forces on the feet (figure 6). These reaction forces give linear momentum to the combined thrower+discus system. Forward horizontal linear momentum is generated in the early stages of the throw. It makes the system translate horizontally across the throwing circle (figure 1, left). During the delivery phase, the thrower loses part of the forward linear momentum and obtains upward vertical linear momentum (Figure 1, right). That is, the forward-moving athlete plants the left foot ahead of the body and presses forward and downward on the ground. This action helps the athlete obtain vertical speed at the expense of some loss of horizontal speed. At release, the thrower+discus system will have some leftover forward linear momentum, as well as upward linear momentum. An analogy that can be used here to explain the purpose of giving forward linear momentum to the thrower+discus system is as follows: One can compare the discus thrower with a ship firing a cannon. If the ship is traveling forward as the cannon is fired, the forward speed of the ship is added to the forward speed of the projectile. This results in a larger total horizontal speed of the projectile as compared to a condition where the ship is static when it fires the cannon. The forward motion of the thrower+discus system contributes to the speed of the discus at release, and the thrower indeed needs to take advantage of this forward motion as much as possible, albeit its limited contribution to the overall speed of the discus at release. ANGULAR MOMENTUM To understand the process of generating the speed of the discus relative to the CM of the thrower+discus system, we will need to look at the angular momentum of the thrower, the angular momentum of the discus, and the angular momentum of the combined thrower+discus system. Although the discus speed is the ultimate goal, one cannot look exclusively at the raw speeds because speed alone does not explain the dynamic relationships between the speed of the discus, the forces made by the thrower on the ground and the motions of the thrower. Essentially, the angular momentum of the thrower+discus system is equal to the angular momentum of the thrower plus the angular momentum of the discus. In other words, the angular momentum of the discus is directly proportional to its speed. By focusing on angular momentum instead of speed, one can gain a mechanical understanding of the discus’s speed development process because the angular momentum of the discus is directly proportional to its speed (Dapena & Anderst, 1997).
The ground reaction forces which produce the linear momentum of the thrower+discus system also give angular momentum to the thrower+discus system. There is angular momentum in two independent directions. First, about a vertical axis (figure 2) and second, about a horizontal axis aligned with the midline of the throwing sector (figure 3). A transfer of angular momentum about the vertical axis from the thrower to the discus imparts horizontal speed to the discus (figure 2), and it also tends to slow down the thrower’s counterclockwise rotation in the view from overhead. A transfer of angular momentum about the horizontal axis from the thrower to the discus imparts vertical speed to the discus (figure 3). It also tends to slow down any counterclockwise rotation of the thrower in the view from the back of the circle (Dapena, 1994 b, 1993 a). Figure 4 shows the net contributions of the momentum generated (linear or vertical) to the final speed of the discus. It also shows that linear momentum contributes minimally, and that angular momentum is the main contributor to the discus speed. The rotation of the thrower+discus system about a vertical axis can be generated most effectively while both feet are in contact with the ground, through a "pull-push" mechanism. There are two such periods in every throw: the first double support phase at the back of the circle and the double-support phase during the final delivery. The roles of these two double-support phases need to be addressed. Some may still emphasize the dynamic delivery phase while the "back of the circle" may be receiving only limited attention. However, discus throwers need to be very dynamic in the parts of the throw that precede the delivery phase. GENERATION OF HORIZONTAL SPEED THROUGH ANGULAR MOMENTUM ABOUT THE VERTICAL AXIS
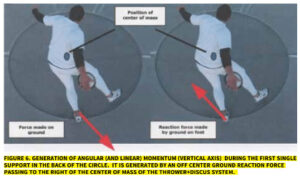
Most of the angular momentum of the thrower+discus system about the vertical axis is obtained from the ground during the initial double support phase at the back of the circle and the following single support phase on the left foot. During the initial double-support phase, the angular momentum is probably generated mainly by pull-push forces (figure 5). During the single-support phase on the left foot, it is generated by an off-center ground reaction force that passes to the right of the CM of the thrower+discus system (figure 6). During the single support over the right foot in the middle of the circle, the right foot generally makes on the ground a small horizontal force, which points forward and somewhat toward the left (figure 7, left). The ground reaction force points almost directly through the CM of the system and therefore, the angular momentum of the system about the vertical axis remains almost constant during the single support on the right foot. A small (but not negligible) amount of angular momentum about the vertical axis is added to the system during the final delivery phase. The increase in the angular momentum of the system about the vertical axis during the final delivery is small, approximately 10%, compared to that generated in the back of the circle (Dapena & Anderst, 1997, Dapena 1994 b, 1993 b). The directions of the forces made by the feet on the ground during the delivery phase are approximated in figure 7, right. The left foot probably pushes on the ground forward and perhaps somewhat toward the right, while the right foot may exert on the ground a smaller force which points backward and toward the left, with respect to the throwing circle. The reactions to these forces produce the observed increase in the counterclockwise angular momentum of the system about the vertical axis during the delivery. This inability of the thrower to generate a large amount of angular momentum about the vertical axis during the delivery phase begs the question as to why it is so. Presumably, the thrower has already been rotating so fast about the vertical axis by the time she reached the middle of the circle during the second single support, that the feet find it difficult to make very large horizontal forces on the ground (Dapena, 1993 a, Dapena & Anderst, 1997). To illustrate, let us consider a downhill skier coming off the gate to start her descent. Along with using her legs actively to move forward, she would also initially stroke with her ski poles very dynamically against the snow surface to help accelerate that descent. However, as the speed of the skier+ski poles system reaches high values a few seconds later, it becomes increasingly difficult and eventually impossible to keep using the poles any longer; so, the skier tucks the poles away and allows gravity alone to take her to the finish line. That is, further use of the ski poles would be a braking force not a propulsive force or, stated somewhat differently, the skier may think that she is helping the system move forward, but she is not. Similarly, discus throwers may think that they are exerting forces against the ground during the delivery phase when they are not; at least not as significant forces as they think (Dapena & Anderst, 1997, Dapena, 1993 a).
The conditions in the back of the circle at the start of a discus throw are analogous to those of an initially motionless skier. From initial static conditions, the subject is able to achieve significant increases in speed by using the ski poles or in angular momentum about the vertical axis (in the early part of a discus throw). The conditions at the start of the double-support delivery phase in the discus throw are analogous to those of a fast-moving skier. When the subject is already moving very fast, it is difficult or impossible to achieve further increases in speed by using the ski poles or in the angular momentum of the whole system about the vertical axis (in the double-support delivery phase of a discus throw). Does the thrower need to make an all-out effort to generate counterclockwise angular momentum about the vertical axis at the back of the circle? Not necessarily. However, there will be a problem if the thrower is not active enough during that period. Another analogy that can help to further elucidate this point (i.e., how active a thrower should be in the back of the circle) is to consider a long jumper, say four steps prior to the end of the run-up. Assuming that the athlete is already running at c. 98% of the desired speed, the athlete probably will not have much difficulty reaching 100% of the desired speed in the four remaining steps. Therefore, running at a somewhat sub-maximum speed a few steps prior to the end of the run-up is not necessarily a problem for the long jumper. On the other hand, if four steps prior to the end of the run-up the athlete were running say, at c. 50% of the target speed, the jumper would not have enough time in the four remaining steps to reach the target speed at the end of the run-up, and the result would be a sub-par jump. In a similar way, if the angular momentum of a discus thrower about the vertical axis is somewhat smaller at the start of the double-support delivery phase, this may not be a problem, because within certain limits, the athlete should have the opportunity to increase that angular momentum to the assumed desired value before release. However, if the value of the same angular momentum is too far below the target value, the thrower will find it impossible to reach the target value before release, resulting in a sub-par throw. It is not known how low the angular momentum about the vertical axis can be at the start of the double-support delivery before it starts to negatively affect the throw. What is known is that the value of the angular momentum about the vertical axis, at the beginning of the double support delivery, is not far below the value that it has at release. This means that although most throwers rely, to some extent, on an increase in the value of that angular momentum of the thrower+discus system during the delivery phase, they actually rely much more on the angular momentum that they generate during the first double support and the early part of the first single support (Dapena & Anderst, 1997). Although the discus thrower needs to generate a large amount of angular momentum around the vertical axis during the early part of the throw, the motions of the athlete at the back of the circle should not be rushed. Instead, during the first double-support and single-support phases, the athlete should rotate at a reasonably fast pace while keeping the arms and the swinging leg widely spread. SPECIFIC MECHANICS OF ANGULAR MOMENTUM GENERATION DURING THE FIRST DOUBLE & FIRST SINGLE SUPPORT At the back of the circle, the thrower wants to generate the maximum possible amount of angular momentum about the vertical axis. It’s emphasized that what a thrower wants is a large amount of angular momentum, not necessarily of angular velocity. To achieve this, the thrower swings the right leg counterclockwise very fast, very far from the middle of the body, and over the longest possible range of motion. Such a thrust of the swinging right leg helps the athlete to generate (i.e., obtain) counterclockwise angular momentum about the vertical axis. Here’s how: Angular momentum is generated by the torques exerted on the body+discus system about the vertical axis. The increase in angular momentum is equal to the amount of torque received from the ground, multi-plied by the time during which this torque is exerted. That is, angular momentum = T (torque) x t (time) and that relationship states that for any given amount of time, the bigger the torque, the bigger the angular momentum the thrower will have in the end. So the thrower wants a maximum value for the products of torque and time. As mentioned earlier, these torques are exerted essentially by "pull-push" forces received by the feet from the ground during the double-support phase (figure 5) and by a more or less forward-pointing force exerted by the ground on the left foot, a force that points slightly off-center to the center of mass in the view from overhead, during the single-support phase (figure 6).
So the thrower wants maximum torque and maximum time. However, if the thrower receives a very large torque from the ground, she tends to rotate quickly (all other things being equal) and if she rotates quickly, the time that she will have available will decrease. So clearly, there is an apparent conflict here. Should the thrower reduce the torque in order to have more time available? The answer is no (Dapena, 2021). The thrower needs to maximize the torque, and when that results in a shortening of the time, so be it. What the thrower needs to do to mitigate the shortening of the time is to increase the time by increasing the range of motion. The way to do this during the "wound up" position in the back of the circle is to start the counterclockwise motion (towards her own left) of the whole system with the discus in the most clockwise (towards her own right) position possible. Of course, discus throwers already do this. At the most clockwise position of the discus, the hips are clockwise relative to the footprints, the shoulders are clockwise relative to the hips, and the discus is clockwise relative to the shoulders. Apart from producing some stretching of muscles, the main goal of this position is to provide more time for the sub-sequent counterclockwise motion through an increased counterclockwise range of motion. So the thrower wants to maximize torque even though it tends to reduce the available time. The question is then whether there is a way to increase the torque. Indeed, there are a couple of ways to produce a big torque; the main way being to exert the muscles very hard. An additional way to increase the muscle forces is by reducing the speed of contraction of the muscles. At the most clockwise position of the discus in the back of the circle, the body is momentarily unmoving. It has been rotating clockwise up to that point, but it will continue moving in a counterclockwise direction, so at that precise point in time, the body is basically at a standstill. That is, it has neither clockwise nor counterclockwise speed of rotation. At that time, the muscles that will propel the athlete in her counterclockwise motion are momentarily (instantaneously) in isometric conditions. In isometric conditions, muscles are able to exert very big forces and therefore, at this time, the thrower will be able to make the ground apply a large counterclockwise torque onto her. Ideally, these muscles would keep exerting those large forces throughout the entire double-support and single-support phases in the back of the circle, because large muscle forces imply large torques exerted by the ground onto the thrower. But there is a problem. The counterclockwise torques exerted by the ground onto the thrower make the thrower rotate faster and faster counterclockwise, and in doing so, it becomes harder and harder to achieve those large muscle forces because the muscles go from isometric conditions (at the most clockwise position of the discus) to slow concentric conditions and, later, to fast concentric conditions. Physiology tells us that the faster the concentric conditions of a muscle, the smaller the force that it can exert. So should the thrower reduce the size of the muscle forces to reduce the increase in counterclockwise angular velocity, therefore putting the muscles in slower concentric conditions, which would then allow the muscles to exert larger forces? No. For the thrower to reduce the muscle force in order to increase the muscle force would be illogical. This is the second apparent conflict. But again, there is a good solution for minimizing this conflict. The muscles need to be kept, at all times, at the maximum tension they can exert. Although that will make the body rotate faster, thus reducing the muscle forces, to a great extent, this is unavoidable. However, the thrower can mitigate the loss of muscle tension by maximizing the system’s moment of inertia, which can be done by keeping the arms outstretched in the double-support and the lead leg outward during the single-support. Under these conditions, for the given amount of angular momentum that the system has, the speed of rotation (its angular velocity) won’t be as large, and the speed of rotation, not angular momentum, is what determines how quickly the muscles contract. The priority in the back of the circle is to increase angular momentum, not angular velocity, and the best way to increase angular momentum is to keep angular velocity as small as possible. Angular velocity should not be kept relatively small by limiting the amount of angular momentum because that would be self-defeating. It needs to be kept small by increasing the moment of inertia, which would allow the thrower to increase angular momentum more quickly from the value that it has at a specific point in time. Succinctly stated, although theoretically one can increase the angular momentum (L) by increasing either the moment of inertia (I) or the angular velocity (ω) since L= I ω, the thrower should always favor an increase of inertia at the expense of angular velocity because both practically and mechanically, it's unwise to increase angular velocity, due to the fact that as velocity goes up, torque goes down because of muscle physiology regarding speed of contraction and tension generation. This inability to generate torque at high speeds is disproportionate enough to justify a loss in speed in favor of an increase in the moments of inertia. TRANSFER OF ANGULAR MOMENTUM Following the generation of the maximum angular momentum possible in the first double and the first single support phases, that rotary momentum is "stored" in the thrower while the discus is given just a small amount of the rotary momentum. The rotary momentum obtained by the thrower and the discus during this first double support phase and first single support phase does not increase during the delivery phase, as explained earlier (Dapena, 1993 a). On the other hand, a powerful transfer of rotary momentum from the thrower to the discus takes place during the delivery phase, which results in an increase in the horizontal speed of the discus. Rotary momentum about the horizontal axis, the major contributor to the vertical speed, is obtained during the second half of the second single support phase and the first half of the delivery phase. At that moment, the thrower receives, from the ground, a force that passes to the right of the CM, and it gives the thrower counterclockwise rotary momentum as viewed from the back of the circle. The momentum is then transferred to the discus and produces majority of the vertical speed of the discus. As with the rotary momentum about the vertical axis, most of the rotary momentum about a horizontal axis is not obtained from the interaction with the ground in the middle of the circle (Dapena, 1993 a). GENERATION OF VERTICAL SPEED OF THE DISCUS THROUGH ANGULAR MOMENTUM ABOUT THE HORIZONTAL AXIS The angular momentum about a horizontal axis aligned with the midline of the throwing sector is important for the generation of the vertical speed of the discus (figure 3). This angular momentum is generated mainly during the second half of the single-support phase on the right foot and during the first half of the delivery phase. During the single support phase, the thrower’s right foot exerts onto the ground a force that points vertically downward and possibly also somewhat toward the left in the view from the back of the circle (figure 9, left). The ground reaction to this force passes to the right of the CM. Since the reaction force is off-center (in other words, it does not point directly through the CM), it gives the thrower counterclockwise angular momentum in the view from the back of the circle. During the early part of the double-support delivery phase, the directions of the forces made by the feet on the ground are not clear. However, it seems that the right foot continues to push on the ground downward and perhaps further toward the left than in the single support (figure 9, right), while the left foot pushes closer to the vertical direction. The reaction force exerted by the ground on the right foot would thus pass to the right of the CM and would tend to increase the counterclockwise angular momentum about the horizontal axis of the system, while the reaction force exerted on the left foot would pass to the left of the CM and would tend to decrease the angular momentum. Overall, the action of the right leg is dominant, and the result is a net gain of counterclockwise angular momentum about the horizontal axis during the first half of the double-support delivery phase. In most throwers, during the second half of the delivery phase there is not much further gain of angular momentum about the horizontal axis. However, part of the counterclockwise angular momentum that has been generated during the second half of the single support phase on the right foot and the first half of the delivery phase is transferred from the thrower to the discus during this period. Again, this transfer of angular momentum during the second half of the delivery phase produces most of the vertical speed of the discus (Dapena & Anderst, 1997). PRACTICAL OBSERVATIONS REGARDING MOMENTUM One may argue that experience teaches that a discus thrower should prefer to execute moderate and rather slow movements in the back of the circle and try to arrive at the center of the circle under control, ready for the all-important final delivery of the discus. It may also seem quite paradoxical to argue that during the dynamic delivery phase in the front of the ring, there is no gain in the rotary momentum of the thrower+discus system, and that the thrower rotates so quickly about the vertical axis that she finds it difficult to exert forces on the ground. Most coaches would argue that the faster a thrower performs the turn in the back of the circle, the higher the risk that there will be a slowing down and poor execution of the delivery phase. In the same fashion, it seems obvious that there should be a tremendous pushing against the ground during the delivery phase. Would it be possible to throw successfully on a slippery surface? Moreover, good discus throwers can throw over 55 meters from a standing position. Since there is no momentum during the start in this type of throw, it is evident that all momentum is generated during the delivery phase because this is what a standing throw is all about. If there was no momentum generation, a throw could not take place (Vrabel, 1994).
Experimental data (Dapena, 1993 a, Dapena & Anderst, 1997) has shown that there is no additional momentum development during the delivery of the discus. Again, the reasoning can be found in that the body is rotating so rapidly during that phase, that the thrower is unable to exert significant forces onto the ground, as illustrated earlier using the downhill skier example. However, although the thrower exerts minimal forces against the ground during the delivery phase, these forces are not zero. A thrower would tend to slip on an icy surface, the same way a distance runner running on an icy road would tend to slip, although the forces exerted against the ground are small. However, in the case of the discus thrower, the tendency to slip would be much greater in the back of the circle, as it would be greater during the first strides of a sprinter as she tries to accelerate (Dapena, 1994 a). As far as the standing throw is concerned, from a dynamic point of view, its execution is different from the execution of the delivery phase. In the standing throw, the thrower creates forces on the ground, which are not present in the delivery phase of a full discus throw. The implication here is that there are certain differences between the muscular actions of a standing throw and those of SUMMARY The dynamic execution of the movements in the back of the circle is of paramount importance for the correct execution of the discus technique. Throwers cannot capitalize on an increase in the rotary momentum during the delivery phase. That momentum has already been generated during the phases of the first double and the early part of the first single Good throwers are not rotating super quickly in the back of the ring, but this does not mean that they are "taking it easy." They have acquired quite a bit of angular momentum and to achieve that, they are making big torques. But the angular momentum is being stored in the form of a big moment of inertia and a relatively small angular velocity, and this relatively small angular velocity is what makes some coaches believe that the athletes are "taking it easy." At the time of the end of the single-support phase at the back of the circle, very little of this angular momentum is stored in the discus or in the throwing arm, so it gives the false impression that nothing very dynamic is going on. Indeed, nothing very dynamic is going on in the discus or the throwing arm, in the back of the circle. That is because all "dynamism" is taking place in the whole body+discus system, of which the throwing arm and discus are very small parts. The throwing arm and the discus don’t get ultra-dynamic until the second double-support (delivery) phase in the front of the circle, when a REFERENCES Dapena, J. (2021). Personal Communication. Dapena, J., & Anderst, W. (1997). Discus Throw (Men). Scientific Services Project, U.S.A Track & Field. Biomechanics Laboratory, Dept. of Kinesiology, Indiana University. Dapena, J. (1994 a). New insights on discus throwing: A response to Jan Vrabel’s comments. Track Technique, 129, 4116-4119. Dapena, J. (1994 b). An analysis of angular momentum in the discus throw. Journal of Biomechanics. 27, 660 Dapena, J. (1993 a). New insights on discus throwing. Track Technique, 125, 3977- 3983. Dapena, J. (1993 b). An analysis of angular momentum in the discus throw. Proc. 14th Cong. ISB, Eds. S. Bouisset, S. Mdtral and H. Monod. Societe de Biomecanique, Paris, 306-307. Vrabel, J. (1994). Are Dapena’s insights on discus throwing correct? Track Technique, 129, 4114-4115. DR. ANDREAS MAHERAS IS THE THROWS COACH AT FORT HAYS STATE UNIVERSITY AND IS A FREQUENT CONTRIBUTOR TO TECHNIQUES. |